原文链接：https://arxiv.org/abs/1706.03762

Intro

RNN（特别是LSTM和GRN）在序列的建模与转换问题上（如语言建模、机器翻译）成为了SOTA方法，因此学者们对循环语言模型 (recurrent language models) 和编码-解码器架构 (encoder-decoder) 进行了大量研究。

循环网络模型考虑了输入和输出序列中，字符的位置来进行计算。循环模型用上一个隐藏状态\(h_{t-1}\)和\(t\)时刻的输入来产生下一个隐藏状态\(h_t\)，也就是将时序信息融入了计算。这种时序模型难以并行化处理，计算性能差。虽然有许多并行化改进的研究，但这个问题仍然非常存在且关键

注意力机制此前已经应用于编码-解码器架构中，用于将编码器的信息有效地传递给解码器，然而这种机制大都与RNN结合使用

本文提出了Transformer架构，不依赖循环网络，而是完全基于注意力机制来建立输入与输出之间的全局关系。Transformer更加支持并行化，并且在更短的训练时间内达到新的SOTA性能

背景

为了减少时序计算的开销，Extended Neural GPU，ByteNet和 ConvS2S这些基于CNN的方法，都并行地计算所有输入和输出位置的隐藏状态

这些模型中，关联任意两个输入或输出位置的数据，所需要的运算次数随着两者之间的距离而增长。在ConvS2S中线性增长，在ByteNet中以对数增长。这就使得关联两个较远位置的数据变得更加困难

引用：“因为卷积计算时，卷积核/感受野比较小，如果序列很长，需要使用多层卷积才可以将两个比较远的位置关联起来）。但是使用Transformer的注意力机制的话，每次（一层）就能看到序列中所有的位置”

在Transformer中，运算次数是以常数随着距离增长的。虽然，因为我们对序列中的各个位置进行了注意力加权的平均，减少了有效解，但我们会用多头注意力机制 (Multi-Head Attention) 来抵消这种影响

引用：卷积的好处是输出可以有多个通道，每个通道可以认为是识别不同的模式。所以作者提出了多头注意力机制，来模拟卷积的多通道输出效果

自注意力 (self-attetion/ intra-attention) 是一种注意力机制，将一个序列中不同位置的数据关联起来，来计算这个序列的一种（数学）表示 (representation)。该机制在阅读理解、抽象总结等方面都得到了成功的应用。

Transformer是第一个完全依靠self-attention，而不使用卷积或循环的encoder-decoder转换模型

模型架构

Overview

encoder-decoder结构：encoder把输入序列\((x_1,...,x_n)\)映射到一个连续的（数学）表示\(\textbf{z}=(z_1,...,z_n)\)。给定\(\textbf{z}\)，decoder就会每次一个元素地产生输出序列\((y_1,...,y_m)\)

个人理解：我在“表示”的前面加上“（数学）”，是因为\(x\)是非数学的字符（如文字），将其转换为数学的字符（如向量中的元素，即数字）后，即为\(z\)

每一步中，模型都是自回归的 (auto-regressive) ，在生成下一结果时，会将之前生成的结果加到输入序列中。（自回归模型，即过去时刻的输出可以作为当前时刻的输入）

Transformer遵循这种架构，对encoder和decoder使用堆叠的自注意力和逐点全连接层，分别如图1的左半和右半部分所示

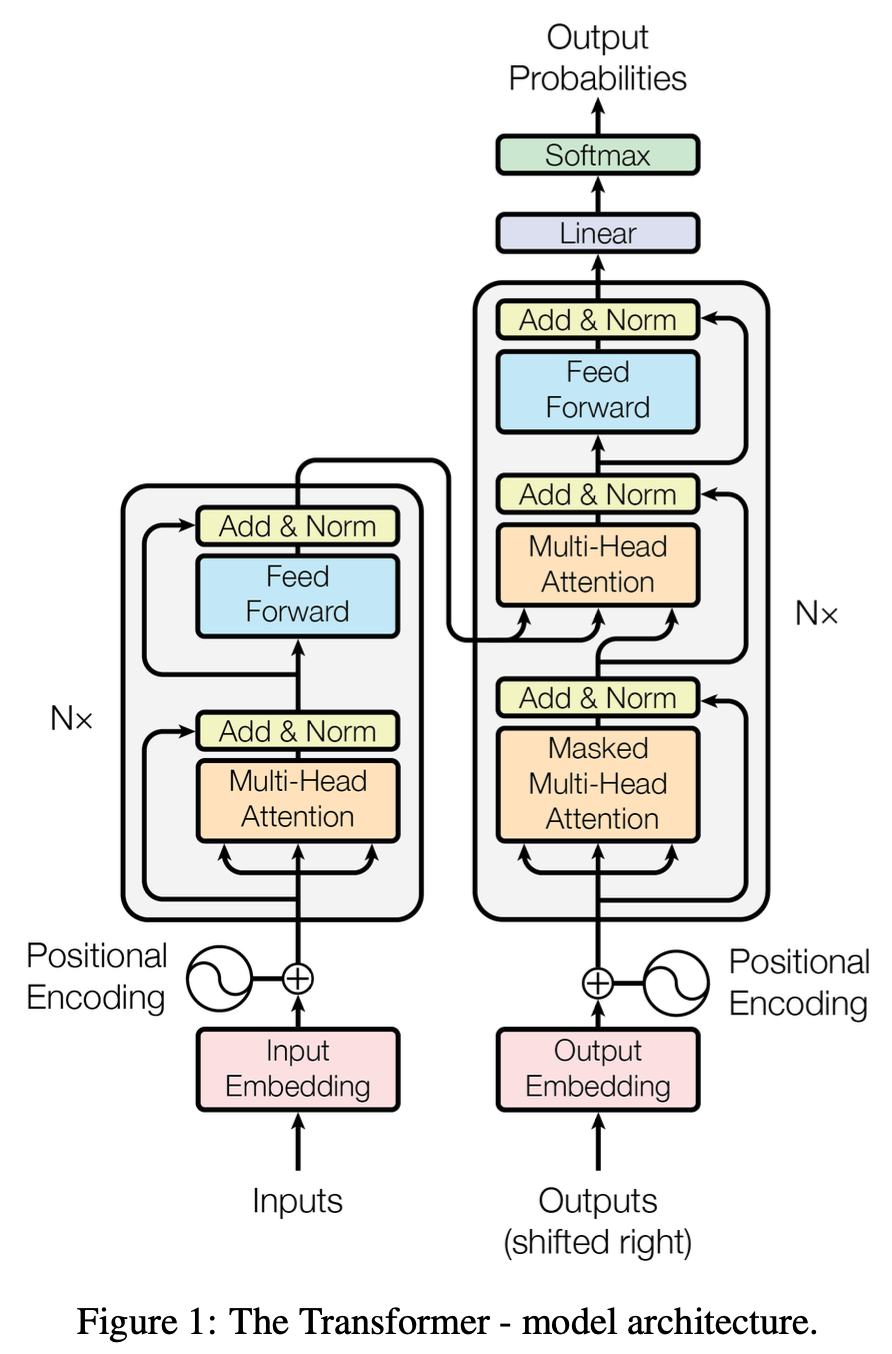
Encoder和Decoder

Encoder

Encoder由\(N=6\)个相同的层组成，每个层有两个子层：

  1. multi-head self-attention
  2. position-wise fully connected feed-forward network

每层后面都使用残差连接 (residual connection) 和层标准化 (layer normalization)。即每个子层的输出为：\[LayerNorm(x+Sublayer(x))\] 所有子层、嵌入层 (embedding layer) 的输出维度都是\(d_{model}=512\)

引用-Layer Norm： 首先看一下Batch Norm，它针对同一个特征来进行Norm（如把均值变为0，方差变为1）；而Layer Norm是针对同一个样本进行Norm。

Batch Norm需要计算全局样本的同一特征，序列长度变化大时，计算出来的均值和方差抖动很大。预测时使用训练时记录下来的全局均值和方差。如果预测时新的样本长度超过训练时的长度，那么超过部分是没有记录的均值和方差的，预测会出现问题

而Layer Norm只需要对该单个样本进行计算，序列变长时，计算的数值更稳定。不需要存一个全局的均值和方差，预测样本长度不影响最终结果

Decoder

Decoder也由\(N=6\)个相同的层组成，每个层有三个子层（多了一个在encoder输出上运用多头注意力机制的层）。同样在每层后面使用残差连接和层标准化

不同之处在于对自注意力模块进行了修改，防止当前位置的输出收到后面位置数据的影响。这样的掩码，加上对输出的嵌入偏移一个位置，确保了位置\(i\)的预测只依赖于位置\(i\)之前的已知输出

注意力机制

注意力函数将一个查询 (query) 和一组键值对 (key-value pairs) 映射到一个输出，输出是这些值的一个加权和，其中每个值的权重由query与相应key的相似度 (compatibility function) 计算

引用-对QKV的理解：K，V的值是不变的。根据不同的Q，去计算这个Q与每个K的相似度，QK相近的时候，相似度会大一些，因此这个K对应的V权重也就大一些。这也就是注意力机制

缩放的点积注意力 (Scaled Dot-Product Attention)

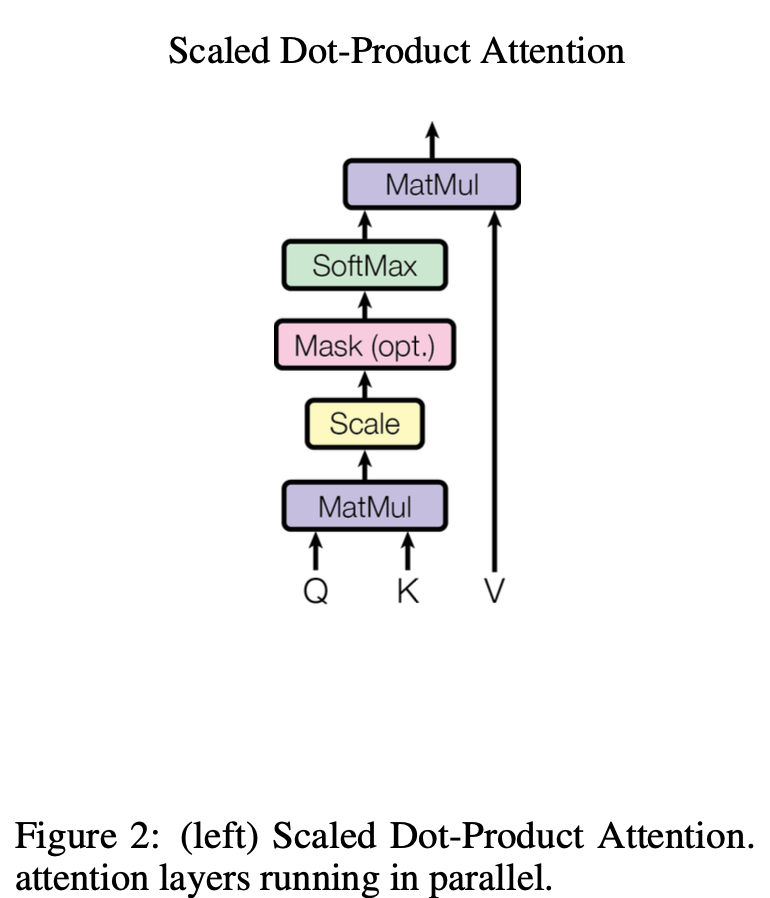
如图。计算过程：

  1. 输入维度为\(d_k\)的 Q (Queries) 和 K (Keys)，以及维度为\(d_v\)的 V (Values)
  2. 计算 Q 和所有 K 的点积（左下的MatMul），得到两个向量的相似度（结果越大相似度越高）
  3. 对每个点积结果除以\(\sqrt{d_k}\)（Scale）
  4. 点积结果输入softmax函数获得V的权重​（SoftMax）
  5. 对V进行加权求和（上方的MatMul）

引用-QK点积：比如两个向量作内积，正交时内积为0，相似度也为0；反之内积值越大，相似度越高。所以此处的QK点积同理

实践中对所有Q同时计算，组成一个矩阵\(Q\)，K和V也组成矩阵\(K,\ V\)，那么注意力矩阵的计算为：\[Attention(Q,\ K,\ V)=softmax(\frac{QK^T}{\sqrt{d_k}})V\]

有两种最常用的注意力函数：加法注意力和点积注意力。除了没有系数\(\frac{1}{\sqrt{d_k}}\)之外，后者与上述注意力函数并无不同。加法注意力使用单个隐藏层的前馈网络 (feed-forward network) 来进行计算。两者在理论复杂度上相似，而实践中点积注意力要快于加法注意力，因为它可以使用高度优化的矩阵乘法

当\(d_k\)较小时，点积和加法注意力性能相当；而\(d_k\)较大时，加法注意力的性能优于不带缩放的点积注意力。我们认为当\(d_k\)较大时，点积的值非常大，导致映射到softmax时梯度非常小，所以使用\(\frac{1}{\sqrt{d_k}}\)来进行缩放

引用-使用Scaled的原因：不缩放的话内积值较大，那么通过softmax之后，大的值就很大，小的值很小（也就是权重的值向softmax的两边靠拢），权重之间的差距变大。而平常使用softmax的目标就是，置信的地方趋近于1，不置信的地方趋近于0，那么这样子就会趋近于收敛，使训练过程难以往下进行

再次阅读之后，个人重新理解一下图2。左侧QK做的运算就是为了计算注意力的权重，计算出来的权重直接与V进行矩阵乘法，就是注意力机制

多头注意力

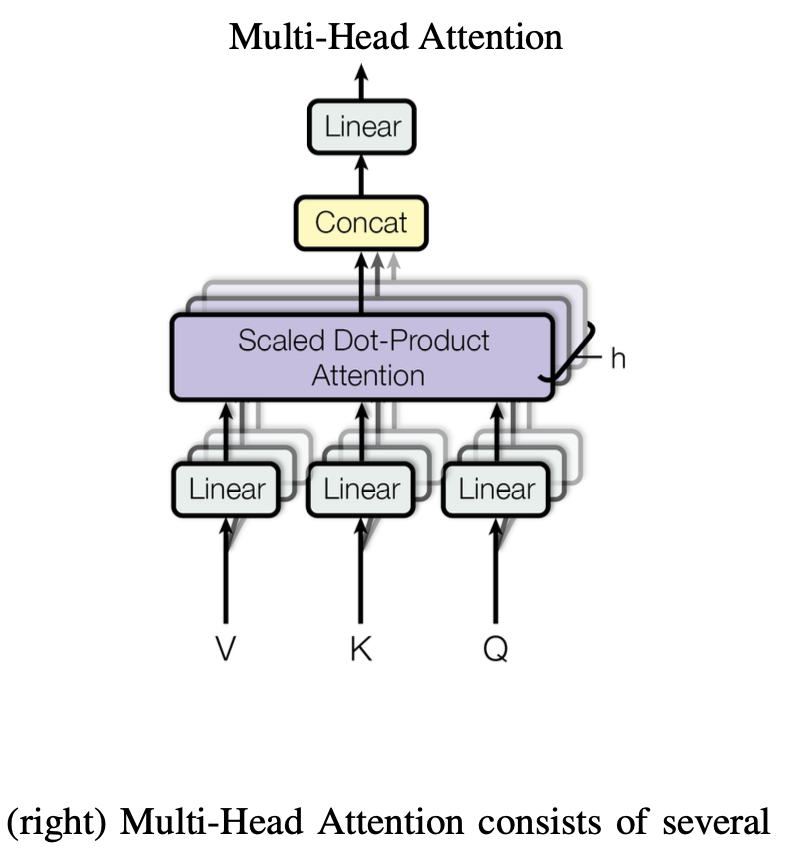
我们将Q, K, V 进行\(h\)次投影，线性投影到\(d_k\)、\(d_k\)和\(d_v\)维度。随后在这些投影上运用注意力机制，产生\(d_v\)维度的输出值，把这些值连接起来再作一次投影，就得到了最终结果值。

引用-多头：把QKV投影h次，到更低的维度，做h次的注意力函数。把每个注意力的输出合并，最后再进行投影。

这个投影的w是可以进行学习的，也就是说，给h次机会，希望能学到不同的投影方法，来匹配不同的模式。所以说类似于CNN，有多个输出通道的感觉

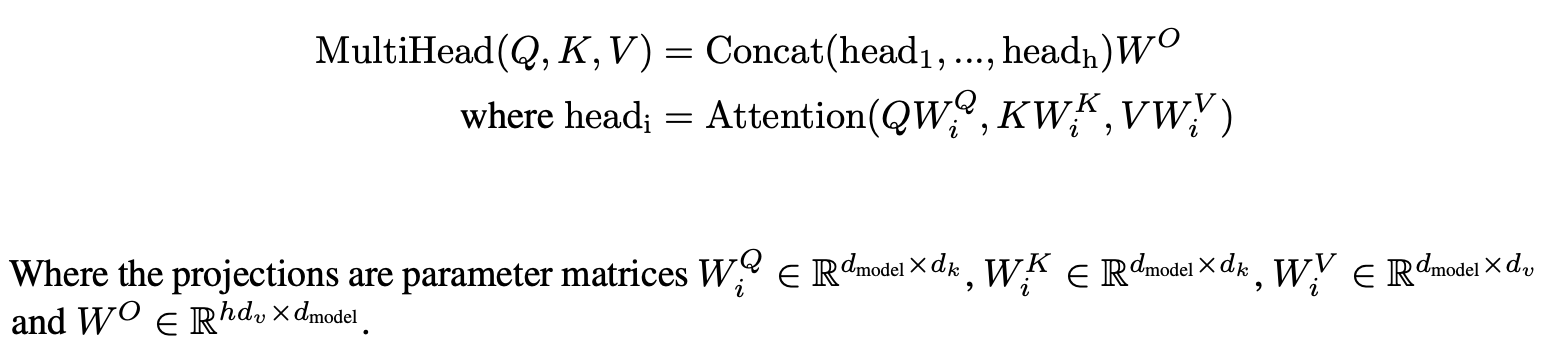
本文参数设置：\(h=8\)，对于每个head有\(d_k=d_v=d_{model}/h=64\)，这样下来，总的计算开销与全维度的单头注意力相似

本模型中注意力的应用

  • encoder-decoder attention ：即decoder的第二个子层。Q来自前一decoder子层，K和V来自encoder的输出。这使decoder中的每个位置都能关注到输入序列中的所有位置
  • multi-head self-attention：即encoder的第一个子层。这使得encoder中的每个位置都可以关注到encoder上一层的所有位置
  • masked-self-attention：用在decoder中，序列中的每个位置只能看到当前位置之前的位置，这是为了保持decoder的自回归特性，防止看到未来位置的信息

引用-自注意力机制：同一个输入复制一下，同时作为KVQ，也就是同一个东西。

在encoder-decoder attention中，Q来自decoder上一子层，而KV来自encoder。那么这个 attention的输出，就是根据encoder输出和decoder上一子层输出的相似性，来对encoder的输出计算加权和（也就是说把encoder的输出，根据Q想要的东西，把它拎出来）

引用-关于Mask：对于\(Q_t\)，这个查询只能看到该时刻之前的信息，所以就只能看到\(K_1,...,K_{t-1}\)。在算好权重并且scale完之后，进入softmax之前，把需要在矩阵中mask的位置都替换成非常大的负数，那么softmax过后，对应的权重就会变成0

基于位置的前馈神经网络（Position-wise Feed-Forward Networks）

encoder和decoder的每一层还包含一个全连接的FFN，对每个位置（上的token）都要做一次以下的变换（包含两个线性变换）：

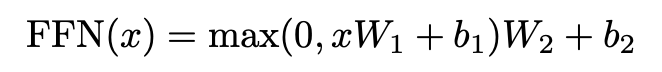
换一种描述方法，其实就是两个卷积核大小为1的卷积层。其中输入和输出的维度为\(d_{model}=512\)，内层维度为\(d_{ff}=2048\)

引用：其实就是一个单隐藏层的MLP，映射到想要的语义空间。其中的max..就是一个ReLU激活层；\(W_1\)将\(x\)映射到2048维，\(W_2\)映射回512维

Point-wise就是指对每个词都做一个同样的MLP。由于经过注意力机制后，输出的向量已经从序列中提取到了想要的信息，所以只需要对每个位置独立做MLP即可。

引用-与RNN的区别：两者都使用线性层/ MLP去做向语义空间的转换。但提取序列信息的方式不同。RNN把上一时刻的输出作为输入，传递给下一时刻；而Transformer通过注意力机制来提取全局的序列信息

嵌入与softmax

我们使用可学习的embedding，将输入和输出转换为\(d_{model}\)​维的向量，并使用线性变换和softmax函数将decoder的输出转换为下一个token的概率

“可学习的”也就是说，这个embedding的方式是一个可学习的参数

此处的softmax前的“线性变换”其实也就是一个embedding

本模型中，（输入、输出）两个embedding层和pre-softmax线性变换所使用的权重矩阵相同。此外，我们将embedding层中的权重乘了\(\sqrt{d_{model}}\)

引用-乘权重的原因：在学习embedding时，会把向量的L2 Norm学成比较小的值（假设为1）。那么当向量的维度一大，为了让L2 Norm学成1，学习时会让权重变小。但之后还要加上位置编码，而位置编码的scale会随着向量长度变大而增大，所以此处乘一下是为了和位置编码保持相似的scale

再换句话：L2 Norm会将向量的所有值归一化，维度越大的向量归一化后，单个元素的值就越小，而时序信息（也就是后面的位置编码）是递增的整数

位置编码

引用：attention不会学习时序信息。也就是说把输入顺序打乱之后，语义已经变化了，但结果是一样的

上述的描述中还缺少对位置信息的嵌入，所以在输入的embedding中加入了位置编码（因为处理语言必须要考虑语序）。其维度与embedding相同，都是\(d_{model}\)，便于两者相加。本文使用以下方式：

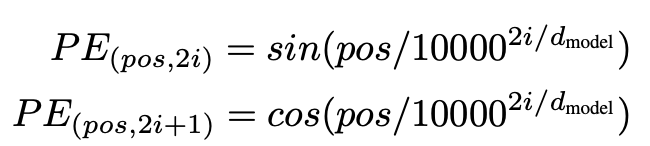
其中\(pos\)是位置，\(i\)是维度。使用这种编码的原因是，作者认为这能让模型易于注意相对位置，因为对于任何偏移量k，\(PE_{pos+k}\)可以表示为\(PE_{pos}\)的线性函数。此外，在遇到比训练数据更长的数据时，这种编码方便模型估计数据的长度=

为什么用自注意力

本节将自注意力与卷积、循环进行了对比。考虑了三个问题：

  1. 每层的计算复杂度
  2. 可并行的计算量，也就是所需的最少顺序计算量
  3. 网络中长距离依赖之间的路径长度。影响学习长距离的依赖的能力的一个关键因素，是前向和后向信号在网络中传播的路径长度。输入和输出序列中任意位置之间的这些路径越短，学习长距离的依赖就越容易。因此，我们比较了由不同层类型组成的网络中，任意两个输入和输出位置之间的最大路径长度

引用：第3点换种说法就是，得到两个位置之间的关系所需要的计算量

其中\(n\)是序列长度，\(d\)是token维度，\(k\)是卷积核大小。可以发现自注意的复杂度更小

引用-restricted的自注意：也就是限制一下范围，只关注最近的r个邻居。但这种方法用得不多

引用：实际上attetion对模型的假设更少，所以需要更大的训练数据量才能达到跟CNN/ RNN相同的效果

训练、实验、结论

略

个人问题与理解

  1. e-d attention为什么是decoder的第二层，不是第一层？

    首先要正确理解注意力。自注意就是对某个序列自身进行查询，得到该序列自己对自己的各个部分的关注度。那么encoder和decoder输入后，都先做一个自注意，得到自注意分数，就便于在encoder的输出中进行查询

  2. mask为什么不是先mask再算权重？

    如果先mask的话，就是对\(Q, K\)做mask。但是QK长宽不一样，而先算权重再mask的话就是对\(QK^T\)做mask，只需要用下三角方阵做mask即可（也就是说对方阵做mask更好做）

（以上为个人理解，不一定对）

参考

https://blog.csdn.net/qq_56591814/article/details/127313216?spm=1001.2014.3001.5502

https://www.bilibili.com/video/BV1pu411o7BE/?spm_id_from=333.999.0.0&vd_source=31c543d6ef0ac6a08fbd17482736f920